18. Atribuir pesos a criterios de evaluación: ¿una trampa?

(Tiempo de lectura: 10 minutos) Atribuir ponderaciones (pesos) a los criterios de evaluación puede ser una trampa cuando no se toma en cuenta las escalas de evaluación asociadas a los correspondientes criterios. Es lo que Ralph Keeney en su libro Value-Focused Thinking llama "el error crítico más común".

¿Quieres verlo?:
"The Most Common Critical Mistake"

También aquí:
"Common Mistakes in Making Value Tradeoffs" 

Explicar este concepto no es fácil. Si no consigo explicarlo adecuadamente, animo al lector a que revise los textos de los vínculos de arriba, y continúe investigando hasta entenderlo, porque esta es la causa de muchas decisiones mal tomadas que traen consecuencias indeseadas.

Lo que deseo expresar es que, en un modelo de evaluación multicriterio por suma ponderada, atribuir arbitrariamente importancias (pesos) a los criterios de evaluación es erróneo, y si no somos conscientes de ello puede llevarnos a engaño, a malas decisiones basadas en razonamiento ilusorio.

La idea principal es que la preferencia relativa entre alternativas no sólo depende de los pesos atribuidos a los criterios de evaluación, sino que depende también de las escalas de evaluación que están asociadas a los respectivos criterios. 

Por consiguiente, cada vez que se nos presente un modelo de decisión multicriterio por suma ponderada (común, común, común en todas las áreas y especialmente en las ciencias sociales), dicho modelo debe venir necesariamente acompañado, además de los pesos de los criterios, de las escalas de evaluación con que se midel esos criterios.

Supongamos que vamos a tomar una decisión sobre la base de cuatro criterios de evaluación: Criterio 1, Criterio 2, Criterio 3 y Criterio 4 y atribuimos a los criterios los siguientes pesos (Tabla 1): El Criterio 1 tendría un peso de 15%, el Criterio 2 un peso de 25%, el Criterio 3 un peso de 40% y el Criterio 4 un peso de 20%. 

- Tabla 1 -

Vamos a tratar de demostrar que podemos manipular los resultados modificando las escalas de evaluación, sin necesidad de modificar los pesos de los criterios. 

Supongamos que utilizamos indicadores cuantitativos para los Criterios 1, 2 y 3, y un indicador cualitativo para el Criterio 4, tal y como se muestra en la Tabla 2. Luego, asociaremos un valor, a través de una Función de Valor obtenida, por ejemplo, aplicando el método Macbeth, a los indicadores para reflejar el grado de satisfacción que aporta cada uno de los niveles de las respectivas escalas. Esto es lo que conocemos como un "Modelo de Valor" o "Modelo de Utilidad".

- Tabla 2 -

En este ejemplo, un nivel de 10 en el indicador del Criterio 1 equivale en términos de satisfacción a un nivel de 40 en el indicador del Criterio 2, y a un nivel de 7 en el indicador del Criterio 3, y a un nivel "Muy fácil" en el indicador del Criterio 4, pues a todos ellos les corresponde un valor de 100 (ver Tabla 2).

Así mismo, sabremos claramente que un nivel de 2.5 en el indicador del Criterio 1 equivale en términos de satisfacción a un nivel de 10 en el indicador del Criterio 2, a un nivel de 4 en el indicador del Criterio 3 y a un nivel de "Difícil" en el indicador del Criterio 4, pues a todos ellos les corresponde un valor de 25 (ver Tabla 2). 

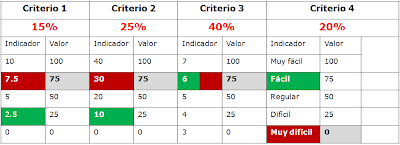
Ahora supongamos que tenemos una alternativa que denominaremos “a” que presenta los siguientes desempeños en los indicadores de los respectivos Criterios (ver Tabla 3, recuadros verdes):

• “2.5” en el Criterio 1;
• “10” en el Criterio 2;
• “6” en el Criterio 3; y
• “Fácil” en el Criterio 4.

- Tabla 3 -

Como puede verse (Tabla 3), al desempeño de 2.5 en el Criterio 1 le corresponde un valor de 25;  al desempeño de 10 en el Criterio 2 le corresponde un valor de 25; al desempeño de 6 en el Criterio 3 le corresponde un valor de 75; y al desempeño de "Fácil" en el Criterio 4 le corresponde un valor de 75. 

Por consiguiente, para calcular el valor global de la alternativa "a", tendremos que multiplicar el valor que dicha alternativa ha obtenido en cada uno de los criterios, por la correspondiente ponderación del criterio, y sumar. Es lo que se conoce como "modelo de agregación aditivo" o por suma ponderada. El cálculo sería así:

• V(a) = 25x0.15 + 25x0.25 + 75x0.40 + 75x0.20 = 55

En este caso, el valor global de la alternativa "a" es 55.

Ahora supongamos que tenemos una alternativa “b” que presenta los siguientes desempeños (Tabla 4, recuadros rojos):

• “7.5” en el Criterio 1;
• “30” en el Criterio 2;
• “6” en el Criterio 3; y
• “Muy difícil” en el Criterio 4.

- Tabla 4 -

Para calcular el valor global de la alternativa "b", tendremos que multiplicar el valor que dicha alternativa ha obtenido en cada uno de los criterios, por la correspondiente ponderación del criterio, y sumar. El cálculo sería así:

• V(b) = 75x0.15 + 75x0.25 + 75x0.40 + 0x0.20   = 60

En este caso, el valor global de la alternativa "b" es 60. Por tanto, podríamos concluir que "b" es mejor que "a", pues el valor de "b" es 60 y el de "a" es 55.

ATENCIÓN ! ! !, que aquí está la trampa en la que podemos caer si no nos percatamos a tiempo:

Pero ahora, ¿qué pasa si disminuimos las expectativas para el Criterio 4? Supongamos que al decisor se le ocurre que somos demasiado exigentes y que pedir un "Muy fácil" en el Criterio 4 es demasiado, es decir, que ahora ya no pediremos “Muy fácil”, sino que nos conformaremos con un “Fácil” en el mejor de los casos en el Criterio 4. Por lo tanto, modificamos la escala del Criterio 4 otorgando un valor de 100 a "Fácil" (que antes tenía un valor de 75, ver Tabla 2 y Tabla 5), y otorgando un valor de 66,66 a "Regular" (que antes tenía un valor de 50), y así con los demás niveles del Criterio 4 como se muestra en la Tabla 5.

NÓTESE QUE LAS PONDERACIONES DE LOS CRITERIOS NO HAN SIDO MODIFICADAS. Sólo hemos modificado los valores de la escala del Criterio 4, como se muestra en la siguiente tabla con la flecha naranja.

- Tabla 5 -

Ahora, los cálculos de valor global tanto para la alternativa "a" como para la alternativa "b" serían:

• V(a) = 25x0.15 + 25x0.25 + 75x0.40 + 100x0.20 = 60
• V(b) = 75x0.15 + 75x0.25 + 75x0.40 + 0x0.20     = 60

¿Qué ha pasado?, pues que la alternativa "b" ya no es mejor que la alternativa "a", y que ahora son iguales, PESE A QUE NO HEMOS MODIFICADO LOS PESOS DE LOS CRITERIOS DE EVALUACIÓN. Hemos logrado morificar los resultados de la evaluación sin necesidad de modificar los pesos de los criterios.

¿Cuál es la conclusión?

La conclusión es que la preferencia relativa entre alternativas no sólo depende de los pesos atribuídos a los criterios de evaluación, sino que depende también de las escalas de evaluación que están asociadas a los respectivos criterios. 

Esto quiere decir que cada vez que se nos presente un modelo de decisión multicriterio por suma ponderada, dicho modelo debe venir necesariamente acompañado, además de los pesos de los criterios, de (1) las escalas de evaluación y (2) los niveles referenciales de las distintas escalas de evaluación. 

En este caso, a causa de dichos "niveles referenciales", sabremos de forma meridianamente clara y transparente que un nivel de 10 en el Criterio 1 equivale en términos de satisfacción a un nivel de 10 en el Criterio 2 y a un nivel de 7 en el Criterio 3 y a un nivel de "Muy bueno" en el Criterio 4 modificado. Así mismo, sabemos que un nivel de de 2.5 en el Criterio 1 equivale en términos de satisfacción a un nivel de 10 en el Criterio 2, y a un nivel de 4 en el Criterio 3 y a un nivel de "Muy malo" en el Criterio 4.

En cuanto a la interpretación correcta de las ponderaciones atribuidas a los Criterios, invito al lector a complementar esta lectura con la siguiente entrada del Blog:

Quinta etapa del Análisis Multicriterio: Ponderar los criterios de evaluación

Espero que guste y sirva. Saludos!